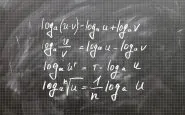I logaritmi sono semplicemente un modo diverso di guardare gli esponenti. Se si dice che il logaritmo della base 5 di 125, o log_5 (125), è uguale a 3, si potrebbe essenzialmente dire che sarebbe necessario innalzare 5 alla terza potenza per ottenere il valore di 125. Talvolta, è necessario per eliminare un logaritmo, in modo da risolvere un problema.
Per fare questo, è necessario sfruttare la seguente regola: b ^ (log_b (a)) = a. Si afferma che una base elevata al logaritmo di b di a è uguale a uno.
I logaritmi
La maggior parte degli studenti italiani, durante gli anni del liceo, ha dovuto fare i conti con i logaritmi. Questi hanno spesso e volentieri rappresentato un vero e proprio incubo per centinaia di alunni. Solitamente i logaritmi si trovano all’interno delle temutissime equazione e rappresentano un modo differente con il quale è possibile analizzare gli esponenti. La loro storia è antichissima. I primi logaritmi infatti risalgono addirittura ai primi anni del 1600. Questi furono introdotti da Nepero che li utilizzò sia nella scienza che nell’ingegneria per riuscire a rendere più semplici calcoli apparentemente molto complessi.
Con i logaritmi inoltre si possono fare numerose trasformazioni. Per esempio da prodotti in somme oppure quozienti in differenze. Attualmente questi logaritmi sono utilizzati maggiormente in tutti i campi matematici ma anche nell’ingegneria e nell’astronomia.
Come eliminarli
La prima cosa da fare per eliminare i logaritmi è quella di cercare di semplificare l’equazione così il logaritmo è di per sé sul lato sinistro. Se avete la log_b equazione (x) – 10 = 0, si dovrebbe semplificare al log_b (x) = 10. A questo punto elevare entrambi i lati utilizzando il b base. Pertanto, l’equazione diventa b ^ (log_b (x)) = b ^ 10. Dopo questi primi passaggi preliminari si può passare all’eliminazione del logaritmo. Utilizzando la regola dell’introduzione, si può quindi ridurre b ^ (log_b (x)) ad appena x. Quindi, l’equazione è diventata x = b ^ 10.
Infine, come ultimo passaggio, bisogna verificare la risposta b assegnando un valore arbitrario. Se si assegna il valore di 3, per esempio, allora x = b ^ 10 diventa x = 3 ^ 10, ovvero x = 59.049. Sulla base di un’equazione dal passo 1 (log_b (x) = 10), il registro di base 3 di 59.049 quindi è uguale 10, che significa elevata alla potenza 10a 3 è 59.049, che è corretto. Come avete visto l’eliminazione dei logaritmi non è quindi una missione eccessivamente complicata. Per riuscire ad eliminarli è infatti sufficiente tanta costanza e un’ottima volontà.